Motivation:

All information in a computer is stored and transmitted as sequences of bits, or binary digits. A bit is a single piece of data which can be thought of as either zero or one. This activity demonstrates how sequences of these two symbols can be used to represent any number.

Materials:

1. Script for your reference, for guiding children to discover binary numbers.
2. Powers-of-2 flash cards and 0/1 cards. for each student. Have the students make these as described below.
3. Large 0/1 flash cards (O on one side, 1 on the other).
4. Copy of the Secret Numbers worksheet for each student.
5. Help Cinda Get To School worksheet for each student.
6. Binary Piano craft worksheets as desired.
7. Binary magic trick handouts as desired.
8. Counting to 1023 on Your Fingers worksheets as desired.

Lesson Plan:

1. The first part of this lesson is a discovery exercise which should stimulate students to learn to count in binary, as well as to reinforce their understanding of place value. You should review the questions in the script before leading the discussion with your students, but don't feel like you have to memorize the whole thing. Keep the script handy! Also note that your discussion will probably not follow the script exactly. It is provided as a guide to help you keep your discussion on track. (The dialogue took place between Rick Garlikov and a class of 3rd graders.)
2. Explain the motivation for the lesson, and tell the students that we're now going to play some games which will give us practice in writing binary numbers.
3. Divide students into small groups (optional - this lesson can be done by individuals, pairs or small groups.).
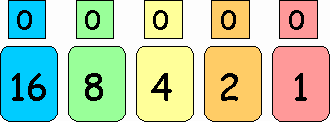
4. Distribute flash cards, one set to each student or group. The first time you do this lesson you'll have to have the students make their cards. The set should look something like this example: (The large cards are approximately 3in x 4in, and the small squares are 2.5in x 2.5in. Note that the small cards have a zero on one side and a one on the other.)

5. Have students sort the cards in descending order so that the largest is on the left and the smallest is on the right.
6. Discussion: "What do you notice about the numbers on the cards?" For the younger kids it is enough for them to notice that 1+1=2, 2+2=4, etc. Middle kids should recognize 1 x 2 = 2, 2 x 2 = 4, etc. High school kids should say something like "powers of 2." They should also note that these are the place values discovered in the preliminary discussion.
7. More discussion (optional):

a. "If I had given you another card, what would it have been?" (32)

b. "How many cards would I have given you if the maximum card were 128?" (8)

8. More optional discussion: Another fun thing to point out is that each card is one more than the sum of all the cards lower than it. For example: 1 + 2 = 3 = 4 - 1, and 1 + 2 + 4 = 7 = 8 - 1. "Without taking the time to add up all the cards, can anyone tell me the sum of all the cards?"
9. Game #1: Have the students turn over the cards so the numbers are hidden. To reinforce their memory of the different place values call out numbers for them to "find." When they seem to know where all the numbers are, with a playful grin call out a number which they don't have. For example, 3. Some students might point out that they don't have 3, but they do have 1 and 2. Do a couple other sums which involve 2 cards, then move to 3 cards, etc.
10. Now flip the cards back over so that the number is showing.
11. Game #2: Call out a number, and have the students place 1s above the cards which sum to that number, and 0s above all other cards. For example, if you say 11, students place 1s above cards 8, 2, and 1, and 0s above 16 and 4. An easy one: 5 (answer 4, 1); harder: 22 (answer 16, 4, 2); last one: 15 (answer 8,4,2,1). If some students find the answers quickly, challenge them to find another solution (they won't be able to do so). Have older kids turn over the flash cards after the first example so they get to practice remembering the values.
12. Ask if anyone in the class has a system for finding an answer. Upper grades should have done so. Request that a student demonstrate the system to the group quickly. (A good method for doing this is to subtract the largest power of two you can from the original number, then subtract the largest power of two you can from that number, then subtract the largest power of 2 you can from that number, etc. until you get down to zero. For example, 37 - 32 = 5, 5 - 4 = 1, and 1 - 1 = 0. Then, write 1s in the places of the powers of two you subtracted and 0s elsewhere: 37 = 100101.)
13. Discussion

a. "What's the largest number you can get?" (31)

b. "What's the smallest number you can get?" (0)

c. "Can you do your age?" (Sure, unless you're older than 31!)

d. "Can you suggest an impossible number which is between the smallest and largest numbers?"

14. Explain that since we know the system we're using is binary, the 0s and 1s represent the original number. Older kids should see the binary expansion as a sum of products where the decimal value is equal to the sum of each binary digit multiplied by its corresponding power of 2.
15. Spend a few minutes reemphasizing the connection between binary numbers to decimal numbers. For example, the decimal value 453 is equal to four 100s plus five 10s plus three 1s. Similarly, the binary value 111000101 is equal to one 256 plus one 128 plus one 64 plus one 4 plus one 1. You may want to point out that just as the place values in the decimal representation are powers of 10, the place values in the binary representation are powers of 2.
16. Game #3: What number is (binary) 11001? 1011? Try to have the advanced students visualize the cards.
17. Can we do all numbers up to the maximum discussed above? To answer this question we need 4 volunteers, each of which holds a large 0/1 card. (We won't go all the way to 31. That would take too long. Instead we'll go to 15.) Each of these 4 students represents one of the flash cards used in the earlier exercises. Have the remaining students direct the 4 students to show 0s or 1s, and sit or stand accordingly. Start with 0, all 4 students should show 0s, and be seated. Next do 1, students should show 0001, and the rightmost person should stand up. Then 2 should be 0010, etc. Try to elicit a system for incrementing the numbers. Point out that this system is like adding 1 each time. Younger kids may not see a system.
18. Discussion: Can all numbers be represented using only 0s and 1s if I gave you enough cards? What's a simple proof of this? (Answer: we can always add 1, so we can start at zero and get up to any number.)

Conclusion:

Closing discussion: briefly discuss with the students what number systems would be like for aliens with different numbers of fingers.

Evaluation:

The first part of this exercise gives the student the opportunity to demonstrate his/her understanding of the mechanics of changing a number to binary and back again.  The second part asks for deeper understanding of the notion of place value. 

Extensions:

Advanced students may be able to prove that a binary representation is unique.

Practice counting to 1023 using only your fingers (up = 1, down = 0). How high can you count if you use your toes as well?

Allow students to discover certain pleasant characteristics of binary numbers. For example, to multiply a binary number by 2, simply add on another 0 in the least significant (rightmost) bit. How can you divide by two? What number is represented by 1? by 11? by 111? by 1111? What is the pattern? What number is represented by 1111111111? Which of these characteristics have analogs in other bases?

What base would an alien use to contact us initially? (Assuming the alien doesn't know that our numeric system is decimal, the alien would use unary (just 1s as a tally of the values).) Suppose the alien counts in base 13. If the it communicated to us in base 13, we wouldn't be able to recognize the values. Higher grade students should be asked to articulate the difference between numbers and their representations.

Have children construct the Binary Piano, or make magic cards for the Binary Magic Card Trick.

Have two students stand apart with 5 chairs between them. Ask one to walk to the other, going left or right around each chair. (See the Help Cinda get to School handout associated with this activity.) How many ways to do this are there? The answer will become more clear if you place a tag on the floor reading "0" to the left of each chair, and reading "1" to the right of each chair, and then ask the children to write down the sequence that they spell out during their walk. How many ways to make a pizza are there, if there are 7 different toppings? (2⁷ = 128, since there are two choices for each topping - either put it on, or leave it off). This extends nicely into a lesson on elementary combinatorics: How many ways are there to get dressed if you can choose between 3 pairs of pants, 5 shirts, and 4 pairs of shoes? (3 x 5 x 4).

Related Links:

• Rick Garlikov's paper on using the Socratic Method for teaching binary numbers

Standards:

• NCTM K-4:  1, 2, 3, 4, 5, 6, 7, 8, 13.
• NCTM 5-8:  1, 2, 3, 4, 5, 6, 7, 8.
• NCTM 9-12:  1, 2, 3, 4, 6, 12, 14.

Skills:

• Problem solving / reasoning / communication / connections
• Whole number addition
• Multiplication by 2
• Place value practice
• Pattern recognition
• Exponents