 Lesson 7: Binary Search
Lesson 7: Binary Search
Motivation:
Computers are often required to retrieve information from large collections of data. For example, a travel agent uses his/her computer to find your travel itinerary from among thousands. It is tempting to think that the machine might as well simply search through all the data until your information is found, but in this activity you will learn a technique which enables computers to search for data much more quickly.Materials:
- Unsorted Find Mag search tableau.
- Sorted Find Mag search tableau.
- Phone book for the city of Pittsville.
- Decision tree for integers between 0 and 63.
Lesson Plan:
- Pointing to one of the troll tableau, tell the students that they can think of the doors as memory locations in a computer, and the numbers on the doors as the addresses of those bits of memory. We can manipulate and change the memory contents by referring to the address, even if we don't know exactly what's inside. Tell them to keep this in the back of their head as we search the doors for trolls...we could be searching memory for something important.
- Tell the students that their goal is to find the troll who has eaten Mag from the row of trolls standing behind doors numbered 1 through 64. The first time you play the game, the trolls will be standing in no particular order. The students ask questions like, "who's standing behind door number 7?"
- Let them query you. They should quickly begin asking you for sequential doors, "who's behind the first door?", "second?", etc.
- Discussion: How long would it take them to find Mag in the worst case? Point out that regardless of what method they used to search, they might have to look behind every door if they were very unlucky.
- Now, play the same game again with the sorted tableau. Explain to the students that the trolls organized themselves in order to help us out, and now they're standing in order, sorted by their names.
- The students are likely to employ the strategy of asking for the name in the approximate middle of the remaining possible space. Notice that this effectively cuts the number of possible locations in half at each step. Keep track of the number of queries required to find Mag.
- Discussion: Once the students have found Mag, discuss the method they were using to search. When one has some idea of how items are distributed, a guess or interpolation is made to try to quickly find the desired item. This is a kind of "binary search", which usually describes the technique of determining which half contains the item sought for by looking at the item in the middle. Lead them to the conclusion that they reduce the number of potential trolls by half at each query, whereas the previous search only reduced the number of trolls by 1 at each query. Ask them why it works - what's the difference between finding an item in a sorted list vs. finding the item in an unsorted list? The answer is simply that we know a lot about where things are if we know a list is sorted. (Tell them that you will teach them about sorting in a future lesson!)
- Have the students play the game again in pairs, if you want, using the Pittsville phone book, or your spelling list, or any other sorted list of items the students find interesting. Have them keep track of the number of queries (of the form "what is item number x?") it takes them to find their item. Let them get some practice playing so that it becomes easier for them to figure out the next best question to ask.
- This is a good time to ask them if they
can think of a relationship between the number of things on the list
and the number of questions it takes them to find something. The
Pittsville phone directory has 128 entries. Can they see why if they
follow the binary search strategy they will never need more than 7
queries? How large of a phone book could they search with 8 queries?
(256: twice as many! First look at the middle element to
determine which group of 128 the desired item is in, and then use the
remaining 7 queries to find it.) How large of a phone book can they
search using 10 queries? (1024).
Point out that the number of queries needed to search a list is at most the number of times you have to halve the number of elements in the list before it reaches 1. Thus, if you start with 1024 items, then
# of questions # of items remaining 1 512 2 256 3 128 4 64 5 32 6 16 7 8 8 4 9 2 10 1 [For older students:] In other words, the number of questions needed is the smallest number n such that 2n = 2 x 2 x 2.... x 2 (n times) is at least the number of items in the original list. (Another name for this value is n = log2 listsize, the log to the base 2, of the number of items in the original list.)]
[For everybody:] A bit of experimentation with this pattern will reveal that even if the number of items is very large, relatively few questions are needed. Can the students name a number that requires more than 100 questions? Did they know that 300 questions would be enough to search a list of size 2300, which is more than the estimated number of protons, neutrons, and electrons in the UNIVERSE!!
Stress the important "rule of halving": The number of times that you need to divide a number by 2 until it reaches 1 is not very many. Later we'll see the "rule of doubling", which says the same thing reversed: starting with 1, only a relatively small number of multiplications by 2 are necessary before a very large number is obtained.
- Finally, if you have already introduced the lesson on binary numbers (Lesson 1), play the game again, but this time the students are to choose a secret number between 0 and 63, and you promise you will be able to guess it in 6 or fewer questions.
- Select a student to choose the number, and let him/her tell the rest of the class (plug your ears).
- Using the decision tree provided, ask questions of the form "Is the number at least ---?". For example, your first question will always be "Is the number at least 32?" The class should answer either "YES" or "NO".
-
Each time you ask a question, write the answer on the board in a
special mysterious way. If the answer is "YES", put a very long
exaggerated tail on the 'Y', and make the 'E' and 'S' very small. If
the answer is "NO", make the 'N' very small and the 'O' very large.
Write the words up-and-down, and line them up so that the long 'Y'
tails and the large 'O's all end up in a line across.
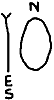
- After you ask (and the class has answered) the 6th question, you'll be able to tell them the secret number. (The secret number is the number you were asking about the last time you got "YES" for an answer.)
- Example: suppose the secret number is 38. Your first question is "Is the number at least 32?", the class answers "YES", and you write the funky "YES" on the board. You ask "Is the number at least 48?", the class answers "NO", and you write "NO". You ask "Is the number at least 40?", the class answers "NO", and you write "NO". You ask "Is the number at least 36?", the class answers "YES", you write "YES". You ask "Is the number at least 38?", the class answers "YES", and you write "YES". Finally, you ask "Is the number at least 39?", the class answers "NO", and you write "NO". The last "YES" answer you got was when you asked about 38, so that must be the secret number.
-
But you may not want to tell them just yet! By now, you have written
the following answers on the board:
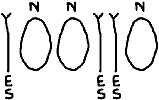
Ask the students if they recognize the binary number that has magically appeared amid the YESses and NOs. It's 38!
- This can lead to interesting discussion. How is it that a '1' in the binary number corresponds to a "YES" answer to one of your questions? Why is it true that the number of queries necessary to find a number equals the length of its representation in binary?
Conclusion:
A fun way to conclude this lesson is to draw a big square on the chalkboard and label it "the desert." Tell the students that there is a lion loose in the desert, and it's our job to build a fence around it so it doesn't hurt anyone. We don't want to catch it any other way, since it's a very cranky lion. How should we do it? Answer: build a fence dividing the desert into two halves. The lion is now in one of the halves. Next, build a fence across the half containing the lion, constraining the lion to one quarter of the desert. Continue building fences across the half of the remaining desert containing the lion, until the lion is cornered. (We've assumed the lion can't get out of the desert.)Talk about the notion of halving: This lesson demonstrates that seemingly difficult tasks can be performed efficiently when, at each stage of the pursuit, the problem can be reduced to a problem half the original size. This technique (reducing the problem to one whose "size" is some fraction of the original problem) is used in many computer programs, not just for searching.
Evaluation:
First, observe all students while they practice the search algorithm on each other, and make sure they all understand it. You may even want to have each group demonstrate their expertise to you while others practice. Listen specifically to the questions they ask, making sure that they essentially split the list in half each time. Second, have the students reflect on their experiences with this lesson. Ask them to tell you two things they've learned, for example, or ask them to describe binary search in writing.Extensions:
Notice that the decision tree we've provided actually queries in a very systematic fashion. Specifically, decreasing powers of 2 are added or subtracted from the previous guess depending on the answer given by the students. From the example above, notice that the first query, 32, is 25. The second query is 32 + 24 or 32 + 16, where the numbers are added because the students said "higher." The third query is 48 - 23, or 48 - 8, where the numbers are subtracted because the students said "lower." As an extension, you could give the decision tree to the students and have them figure out why it uses the queries it does (it uses the method we just described).Have the students play the binary search game using the phone book in pairs, keeping track of the number of queries they used to find a name. After they're finished, ask if anyone can suggest a way to estimate the total number of people in the phone book based upon the querying data from the whole class.
What happens if we can ask which third of the sorted list the item lies in. How many questions do we expect to ask if the list has 500000 elements? (Answer: 12)
Standards:
- NCTM K-4: 2, 3, 4, 5, 6, 7, 8, 13.
- NCTM 5-8: 2, 3, 4, 5, 6, 7, 8.
- NCTM 9-12: 2, 3, 4, 6, 12, 14.
Skills:
- Problem solving / reasoning / communication / connections
- Strategy development
- Whole number addition and subtraction
- Dividing by 2
- Logarithms
- Estimation
- Pattern recognition
- Binary number practice and reinforcement
- Comparison of 2 items: numbers, words, anything.
Copyright (c) 1998, C. Heeren, T. Magliery, and L. Pitt. This lesson and supporting materials may be copied for nonprofit educational use only.