|
|
|
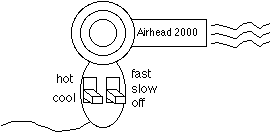
Let's design a finite state machine that models the behavior of a hair blower. Here are the specifications:
Inputs: The inputs to the hair blower can be thought of as applying force to the switches in a given direction. So, we would have 4 inputs: Push up on the left button (let's call this "L-up"), push down on the left button (L-down), and similarly for R-up and R-down.
Outputs: This machine will be slightly different than the ones we've seen so far, in that the previous machines had a singular output that was received in response to an input. Here, the push of a button will cause, say, air to be output, but not just one "chunk" of air. Instead, it makes more sense to think of the machine as being "in the (continuous) state of blowing air", until another input is received. Consequently, we will have NO outputs, but instead we'll label the states to indicate what the hair blower is doing at any given time.
States: As just explained, the states of the machine should reflect exactly what the hair blower is doing at a given time. Thus, there would be one state called "blowing hot air fast", another one for "blowing hot air slow", etc. Hint: make a state for each possible arrangement of the switches. (How many are there? Answer: 6.)
Transitions: The machine should behave as you suspect. For example, if it was blowing hot air slow, and the input L-down were received, then it should next be in the state of blowing cool air slow. Note: If L-down were received again, then since there is nothing cooler than "cool", the machine's behavior would not change - it would stay in the same state. This would be like trying to force the button down further than it can go. (Perhaps we could add a state for "broken").
On the reverse side, or on a separate piece of paper, draw a state diagram for the Airhead 2000.