Motivation:

In this lesson we investigate the problem of coloring maps with as few colors as possible so that no regions sharing a common border are colored the same color. While this seems to be a recreational problem, it turns out that many natural and important problems can be recast as map coloring problems. This lesson is a slight variation on the poor-cartographer lesson in Computer Science Unplugged, and uses some of the same materials.

Materials:

1. Colored overhead markers.
2. Several different maps for coloring: Kootenay, Kaslo, Kamelot, and Krazy - one copy of each map per pair of students. Also, it will be helpful to have an overhead with Kootenay on it.
3. Plenty of markers or tokens of at least 6 different colors.

Lesson Plan:

1. Explain the challenge to the students: A mapmaker wants to use as few colors as possible to color the map of Kootenay, but no two neighboring countries can be colored the same color. Show the map of Kootenay on the overhead, and explain what it means for neighbors to be different colors. Specifically, point out that if countries meet at a point (there are a number of such pairs on this map) then , they are not considered neighbors. (Is Colorado a neighbor of Arizona? Is Utah a neighbor of New Mexico? No. These states meet in the Four Corners.)
2. Have the students work in pairs. It's more fun!
3. Demonstrate with colored tokens on the map of Kootenay that 6 or 7 colors is enough. Suggest that fewer is possible. Who can color it with the fewest number of colors? (2 colors is sufficient. If they have trouble reaching this conclusion, suggest that they start in some corner, and color the adjacent regions one by one, eventually expanding to include the entire graph. Doing it this way, each next decision is forced.) They should use tokens for coloring, rather than crayons in case they change their mind about a color.
4. Give the students the map of Kaslo to color. After a few minutes, ask them how many colors they need. The best possible is 3 colors. Ask how they know that 2 colors is not enough? One argument that 3 colors are required is to point to 3 regions such that each shares a border with the other two. Other, more involved, arguments are possible. However, arguing that a particular region is next to two others is not alone a convincing proof; note that in a country whose states are arranged in a checkerboard pattern, each of the squares on the inside borders with four other squares (left, right, above, below), yet the entire "country" is colored with just two colors (remember that diagonally touching states are allowed to be the same color).
5. Next challenge the students to color Kamelot. Ask them how many colors they need. Have them work until they conclude that 4 is the best they can do. (Which is true.) Ask them if they're SURE 3 isn't enough.
6. Can they argue why 4 are needed? In this case, there are not 4 regions, each pair of which shares a common border. (4 "all next to eachother"). Nonetheless, the constraints imposed by the geography still requires 4 colors. Here is the type of argument to encourage: "These three all touch eachother, so I need at least colors red, blue, and green. Then to avoid coloring this next one yellow (a 4th color), since it is next to the red and blue, I must color it green. But then this other one must be red, because...., and so, ... but then I would need a 4th color over here."

   A simpler argument (which will probably be harder to find) is the following: "The region with the 5 evergreens is the inside of a circle formed by 5 other regions. We need to use red, blue, and green for the circle of 5, since alternating red-blue-red-blue-red leaves the first and last (which are next to eachother in the circle) the same color. But the 5-evergreen region touches all of the regions of the circle, so must be different than red, blue, and green". What is important here is not that they can argue completely why 4 colors are necessary, but that they can follow a chain of reasoning logically to a conclusion.

7. Finally, give them the map of Krazy. This is the hardest map to color. See who can do it in the fewest colors. After they have worked for a bit, tell them it can be done in only 4 colors.
8. If students finish all the maps early, challenge them to create a map which requires 5 different colors. (They can't do it. All maps can be colored by 4 colors.)

9. At this point, if you have done the lesson on graphs, take one of the simpler maps, like Kaslo, and draw the graph that corresponds to the map. (Each region is a vertex, and two vertices are connected by an edge if the regions they represent share a boundary. The graph for Kaslo looks like this:

   

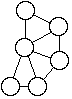
10. Point out now that the map coloring problem corresponds to the problem of coloring the six vertices of the Kaslo graph, so that no two vertices that are connected by an edge are colored the same color. Show how to do this by coloring in the vertices with three colors.

11. Refer now to Example 10 (Prof. Appel's exam-schedule problem), from the handout on using graphs from Lesson 10 on graphs. Use the example to point out how the exam scheduling problem is exactly the graph coloring problem. Mention that there are many other problems that don't appear to be graph coloring problems, or even graph problems at all, but are in fact a disguised version of the graph coloring problem.

Conclusion:

Point out that for planar (flat) maps, such as the ones we've looked at, 4 colors are always sufficient. (This is the famous "Four-color Map Theorem"). Four are also sufficient for maps on a sphere (globe), but it turns out that 4 colors are NOT sufficient in many cases. For example, 5 colors are needed to color some maps on a torus (donut shaped surface). Have the students try to draw a map on a donut-world that needs 5 colors.

Evaluation:

Avoid the temptation to assess students' understanding using their success, or lack thereof, coloring the Krazy map. While coloring the map does require some logical and sequential thinking (in the same sense that every map does), a successful solution is often the result of fortunate observation or just plain luck. It is much more important that they be able to explain their reasoning and solution techniques clearly and concisely.

Extensions:

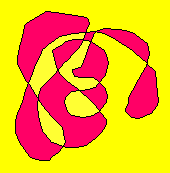
Standards:

• NCTM K-4:  1, 2, 3, 4, 9, 13.
• NCTM 5-8:  1, 2, 3, 4, 8.
• NCTM 9-12:  1, 2, 3, 4, 12, 14.

Skills:

• Problem solving / reasoning / communication / connections
• Strategy development
• Sequential logical reasoning (cause and effect)
• Spatial sense
• Constraint propagation